Induksi Matematika
Induksi matematika merupakan materi yang menjadi perluasan dari logika matematika. Logika matematika sendiri mempelajari pernyataan yang bisa bernilai benar atau salah, ekivalen atau ingkaran sebuah pernyataan, dan juga berisi penarikan kesimpulan.
Induksi matematika menjadi sebuah metode pembuktian secara deduktif yang digunakan untuk membuktikan suatu pernyataan benar atau salah. Dimana merupakan suatu proses atau aktivitas berpikir untuk menarik kesimpulan berdasarkan pada kebenaran pernyataan yang berlaku secara umum sehingga pada pernyataan khusus atau tertentu juga bisa berlaku benar. Dalam induksi matematika ini, variabel dari suatu perumusan dibuktikan sebagai anggota dari himpunan bilangan asli.
Ada tiga langkah dalam induksi matematika yang diperlukan untuk membuktikan suatu rumus atau pernyataan. Langkah-langkah tersebut adalah :
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = 1.
- Mengasumsikan bahwa rumus atau pernyataan tersebut benar untuk n = k.
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = k + 1.
Untuk menerapkan induksi matematika, kita harus bisa menyatakan pernyataan P (k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk meyatakan persamaan P (k + 1), substitusikan kuantitas k + 1 kedalam pernyataan P(k).
Induksi matematika merupakan materi yang menjadi perluasan dari logika matematika. Logika matematika sendiri mempelajari pernyataan yang bisa bernilai benar atau salah, ekivalen atau ingkaran sebuah pernyataan, dan juga berisi penarikan kesimpulan.
Induksi matematika menjadi sebuah metode pembuktian secara deduktif yang digunakan untuk membuktikan suatu pernyataan benar atau salah. Dimana merupakan suatu proses atau aktivitas berpikir untuk menarik kesimpulan berdasarkan pada kebenaran pernyataan yang berlaku secara umum sehingga pada pernyataan khusus atau tertentu juga bisa berlaku benar. Dalam induksi matematika ini, variabel dari suatu perumusan dibuktikan sebagai anggota dari himpunan bilangan asli.
Ada tiga langkah dalam induksi matematika yang diperlukan untuk membuktikan suatu rumus atau pernyataan. Langkah-langkah tersebut adalah :
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = 1.
- Mengasumsikan bahwa rumus atau pernyataan tersebut benar untuk n = k.
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = k + 1.
Untuk menerapkan induksi matematika, kita harus bisa menyatakan pernyataan P (k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk meyatakan persamaan P (k + 1), substitusikan kuantitas k + 1 kedalam pernyataan P(k).
Jenis Induksi Matematika
Sebagai ilustrasi dibuktikan secara induksi matematika bahwa 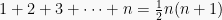 .
.
- Langkah 1
untuk n = 1, maka :
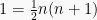

1 = 1
Bentuk untuk n = 1 rumus tersebut benar.
- Langkah 2
Misal rumus benar untuk n = k, maka:

- Langkah 3
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Sehingga:

Pembuktiannya:
 (dalam langkah 2, kedua ruas
(dalam langkah 2, kedua ruas
ditambah k + 1)
![= \frac{1}{2}k (k + 1) +\frac{1}{2} [2(k + 1)] = \frac{1}{2}k (k + 1) +\frac{1}{2} [2(k + 1)]](https://s0.wp.com/latex.php?latex=%3D+%5Cfrac%7B1%7D%7B2%7Dk+%28k+%2B+1%29+%2B%5Cfrac%7B1%7D%7B2%7D+%5B2%28k+%2B+1%29%5D+&bg=f9f9f9&fg=000000&s=0) . (k + 1) dimodifikasi menyerupai
. (k + 1) dimodifikasi menyerupai  )
)
![= \frac{1}{2}[k(k + 1) + 2(k + 1)] = \frac{1}{2}[k(k + 1) + 2(k + 1)]](https://s0.wp.com/latex.php?latex=%3D+%5Cfrac%7B1%7D%7B2%7D%5Bk%28k+%2B+1%29+%2B+2%28k+%2B+1%29%5D&bg=f9f9f9&fg=000000&s=0) (penyederhanaan)
(penyederhanaan)
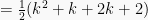

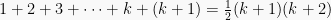 (terbukti)
(terbukti)
silahkan isi absen disini
Sebagai ilustrasi dibuktikan secara induksi matematika bahwa .
- Langkah 1
untuk n = 1, maka :
1 = 1
Bentuk untuk n = 1 rumus tersebut benar.
- Langkah 2
Misal rumus benar untuk n = k, maka:
- Langkah 3
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Sehingga:
Pembuktiannya:
(dalam langkah 2, kedua ruas
ditambah k + 1)
. (k + 1) dimodifikasi menyerupai
)
(penyederhanaan)
(terbukti)
silahkan isi absen disini







Fiska Oktasari-Hadir
BalasHapusDINA AMANDA
BalasHapusAni Anggraini hadir
HapusAni Anggraini hadir
HapusPutri Ishomatus Sya'diah_hadir
BalasHapusMarni Sulis Tia , hadir
BalasHapusDeny aprian , hadir
BalasHapusMelisa tri aulia, hadir
BalasHapusFILDA DWI ANGGRAINI, HADIR
BalasHapusINTANIAS PUTRI-Hadir
BalasHapusSri Wulandari-hadir
BalasHapusNopita sari - hadir
BalasHapusMaimunah-hadir
BalasHapusNATASYA MELINDA-Hadir
BalasHapusDinda varazena-hadir
BalasHapusNadia eprida yunara- hadir
BalasHapusRita Novitasari-hadir
BalasHapusSiti fatmasari hadir
BalasHapusUnknown 22 Juli 2020 21.32
BalasHapusCandra yuhanes
umi zubaidah_hadir
BalasHapusMasriah~hadir
BalasHapusMasriah~hadir
BalasHapusSlamet-hadir
BalasHapusRatna aini hadir
BalasHapusSandya lisbet febriani br hombing-hadir
BalasHapusAni Anggraini hadir kls XI ips2
BalasHapusNovan saputra xl iis 2
BalasHapusEnggal Wahid fauzi hadir 11 IPS 2
BalasHapus